Estimating the Canopy Fraction in your IRR Field of View
A common problem many individuals face when making canopy temperature measurements with an infrared radiometer (IRR) involves estimating the fraction of the field of view that is occupied by canopy (leaves and stems) and soil. This is important in many settings, because plants do not completely cover the ground and the resulting IRR temperature measurement will be a weighted average of canopy components and soil in the IRR field of view. Estimation of field of view occupied by canopy is particularly important early in the growing season when crops are small and a large fraction of soil is viewed. However, knowledge of field of view composition is important in any application where a uniform surface is not being measured due to different surface components. In this case, canopy and soil will typically have different temperatures. The equation to approximate the fraction of IRR field of view occupied by the canopy (fc) is dependent on plant leaf area and is based on the equation to calculate the canopy extinction coefficient for direct beam radiation [1] and is given as:
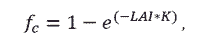
where LAI is the leaf area index, and K is the extinction coefficient. K is dependent on two additional variables: the leaf angle distribution parameter (X) and the viewing angle (θ) of the IRR (relative to nadir view = 0°), which is chosen by the user. These variables will be described briefly below. For more help planning the viewing angle of your IRR, click here.
Leaf Area Index (LAI): Area of leaves per unit area of ground [m2 m-2], which can be expressed as total leaf area or one-sided leaf area. One-sided leaf area (projected area) is half of the total leaf area and is often called hemi-surface area. LAI is typically reported as hemi-surface area per unit ground area, unless the canopy is largely made up of needle-leaf species. In cases where LAI is not directly measured, it is often approximated from canopy height. A few examples from scientific literature are given in the table below.
| Crop | LAI Equation (where h is in meters) |
| Clipped Grass [2] | = 24 * h |
| Alfalfa [2] | = 5.5 + 1.5 * ln(h) |
| Corn [3] | = exp(1.64 * ln(.141 *h)) |
| Soybean [3] | = exp(2.38 * ln(4.17 * h)) |
Extinction Coefficient (K): Area of shadow cast on a horizontal surface by the canopy divided by the area of leaves in the canopy, or in other words, the average projection of leaves onto a horizontal surface. The following equation can be used to approximate K:
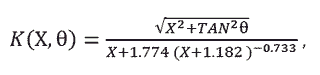
Leaf Angle Distribution Parameter (X): Ratio of average projected area of canopy elements on a horizontal surface to projected area on a vertical surface. X defines the distribution of leaf inclination angles in a plant canopy from 0 (horizontal) to 90 degrees (vertical). For plant canopies with more horizontally-oriented leaves, X is greater than one, and for plant canopies with more vertically-oriented leaves, X is less than one. X = 1 is a good approximation for many plant canopies because leaf area is distributed fairly uniformly among all leaf inclination angles. The figure below shows the inclination angle density for three canopies [4]. The larger X, the more horizontal the leaves are. The equation for these distributions is given by Campbell [5].
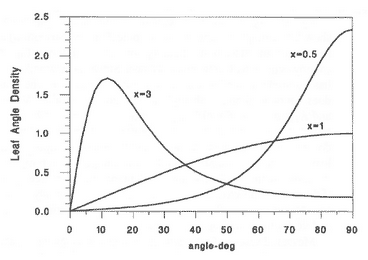
Additionally, X values for various crops have been estimated as shown in the table below [4].
| Crop | X |
| Ryegrass | 0.67-2.47 |
| Maize | 0.76-2.52 |
| Rye | 0.8-1.27 |
| Wheat | 0.96 |
| Barley | 1.20 |
| Timothy | 1.13 |
| Sorghum | 1.43 |
| Lucerne | 1.54 |
| Hybrid swede | 1.29-1.81 |
| Sugar beet | 1.46-1.88 |
| Rape | 1.92-2.13 |
| Cucumber | 2.17 |
| Tobacco | 1.29-2.22 |
| Potato | 1.70-2.47 |
| Horse bean | 1.81-2.17 |
| Sunglower | 1.81-4.1 |
| White clover | 2.47-3.26 |
| Strawberry | 3.03 |
| Soybean | 0.81 |
| Maize | 1.37 |
| J. artichoke | 2.16 |
A simple widget in the IRR product section on our website can help make the necessary calculations to estimate the fraction of canopy viewed by an IRR.
[1] Campbell, G.S. (1986) Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agricultural and Forest Meteorology 36:317-321.
[2] Allen, R.G., et al. (2001) The ASCE Standardized Reference Evapotranspiration Equation. Pg B-6. http://www.kimberly.uidaho.edu/water/asceewri/appendix.pdf.
[3] M.C. Anderson, et al. (2004) Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and Landsat imagery. Remote Sensing of Environment 92:447-464.
[4] Campbell, G.S. and Norman, J.M. (1998) An Introduction to Environmental Biophysics, 2nd ed. pg 250-253.
[5] Campbell, G.S. (1990) Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agricultural and Forest Meteorology 49:173-176.
